浅谈机器学习(1)－Self-Information(自信息), Entropy(熵), Information Gain(信息增益)

说到Self-Information, Entropy, information gain, 我们不得不谈一谈20世纪最伟大的科学家之一，克劳德·香农(Claude Elwood Shannon)，当代信息论的奠基人。他一生中提出过很多伟大的理论，其中信息论的提出，解决了通信理论的很多难题，在次基础上很多不同的应用也被建立起来。

香农理论中，最重要的部分就是entropy的概念。Entropy曾经是波尔兹曼在热力学第二定律引入的概念，用来衡量一个系统的能量有多少被用来作为有用功，有多少可能转化为无效的热量。从分子运动论的观点看，作功是大量分子的有规则运动，而热运动则是大量分子的无规则运动，因此entropy也可以理解为分子运动的混乱程度。在信息论中，entropy被引申用来衡量随机变量的不确定程度。

众所周知，物体的重量可以用天平来衡量，物体的热量也可以用焦耳等单位来测量。可是对于文字，声音和视频，这些乘载信息的媒介，可不可以用一种统一的方式来衡量这些媒介的信息量。香农entropy的作用就是用来衡量一段媒介中所包含信息量的平均大小。例如，中文entropy是9.65比特，英文entropy是4.03比特。这表明中文的复杂程度高于英文，反映了中文词义丰富、行文简练，但处理难度也大。同时，香农entropy也代表了一段信息能够被无损压缩的上限值。

香农定义了一个独立随机变量的Entropy \(H\),
\[H(X)=E(I(X))\]其中，\(E\)是\(I\)的期望，\(I\)是X的自信息量,也就是所谓的self-information。

衡量一个自信息量self-information的大小必须满足以下几个条件:
1.一个随机变量\(x_{i}\)的信息量只依赖于这个随机变量\(x_{i}\)的概率\(p_{i}\)，与它本身的内容是没有关系的,其中:
\[\sum_{i=1}p_{i}=1\]
2.Self-information是一个\(p_{i}\)的连续函数。
3.Self-information是一个\(p_{i}\)的减函数。
4.如果\(p_{i}=p_{i,1}*p_{i,2}\),那么\(I(x_{i})=I(x_{i,1})+I(x_{i,2}).\)
符合以上条件的只有“logarithmic”函数，因此self-information可以定义为:
\[I(x_{i})=-log(P_{i})\]
因此Entropy可以定义为:
\[H(X)=\sum_{i=1}^{n}p(x_{i})I(x_{i})=-\sum_{i=1}^{n}p(x_{i})log_{b}p(x_{i})\]
其中，b是对数logarithm的底。当\(P(x_{i})=0\)的时候，\(0log_{b}0\)被定义为等于0,与其极限条件一致:
\[ lim_{p \rightarrow 0+}
plog_{b}p = 0\]

如果对数log以2为底，计算出来的Entropy就是以bit为单位。而在计算机和数字通信领域，也都是以2进制作为基本单位，所以Entropy的概念可以被广泛的应用到计算机和通信领域。Self-information(信息量)可以被定义为随机不确定程度的减少，换句话说，信息是用来减少随机不定性的变量，也就是信息是确定性的增加。

假设一个独立随机变量X有四个可能的值\({A, B, C, D}\), 它们的分布为:
\[P(X=A)=1/4, P(X=B)=1/4, P(X=C)=1/4, P(X=D)=1/4\]
一个字符序列:BAACBADCDADDDA..符合上面的分布:
我们要把这段字符用二进制的通道传输出去，可以把这四个字符分别编码为(A=00, B=01, C=10, D=11)。
0100001001001110110011111100...
平均每个字符需要2bits来传输

如果这四个值的概率分布不是一样的，新的分布如下:
\[P(X=A)=1/2, P(X=B)=1/4, P(X=C)=1/8, P(X=D)=1/8\]
如果我们把编码变成(A=0, B=10, C=110, D=111),
每个字符的平均长度会变成: 1/2*1+1/4*2+1/8*3+1/8*3=1.75bits

如果给定的一个随机变量\(X={V_{1}, V_{2}, ..., V_{m}}\)的分布,
\[P(X=V_{1})=p_{1}, P(X=V_{2})=p_{2}, ..., P(X=V_{m})=p_{m}\]
基于X的分布，每个字符需要编码成最小的比特数是什么？答案就是随机变量Entropy的大小。
\[H(X)=-p_{1}log_{2}P_{1}-p_{2}log_{2}P_{2}-..-p_{m}log_{2}P_{m}=-\sum_{j=1}^{m}p_{j}log_{2}p_{j}\]

如果随机变量\(X\)的Entropy的值越大，说明这个随机变量\(X\)不确定程度越大，需要把它编码成二进制代码量也越大。从上面的例子可以看出如果随机变量的分布越是不对称，其Entropy值也越小，也意味着这个随机变量可预测性也相对来说较高。

在介绍Information Gain之前，必须先介绍以下Canditional Entropy(条件熵)\(H(Y|X=v)\)的概念。
先看一下，下面的例子，X＝College Major, Y= Likes

College Major	Likes
Math	Yes
History	No
CS	Yes
Math	No
Math	No
CS	Yes
History	No
Math	Yes

从这个表格中，可以得出：
\(H(X)=-1/2log_{2}1/2-1/4log_{2}1/4-1/4log_{2}1/4=1.5\)
\(H(Y)=-1/2log_{2}1/2-1/2log_{2}1/2=1\)
Conditional Entropy可以被定义为:
\(H(Y|X=v)\)在随机变量\(X\)已经给定值\(v\)的情况下，\(Y\)的Entropy大小,也可以解释为当两边通信端都已经了解\(X\)的值为\(v\)的时候，传输\(Y\)的时候，平均需要多少比特。所以，\(H(Y|X)\)可以被定义为:
\[H(Y|X)=\sum_{j}Prob(X=v_{j}H(Y|X=v_{j}))\]
从上面的例子可以看出:
\(H(Y|X=Math)=-1/2log_{2}1/2-1/2log_{2}1/2=1\)
\(H(Y|X=History)=0\)
\(H(Y|X=CS)=0\)
\(P(X=Math)=0.5\)
\(P(X=History)=0.25\)
\(P(X=CS)=0.25\)
\(H(Y|X)=0.5*1+0.25*0+0.25*0=0.5\)

下面我们就可以介绍一下Information Gain(信息增益)的概念。
Information Gain就是当通信两边都知道随机变量\(X\)的时候，平均每个字符可以省下多少比特。
\[IG(Y|X)=H(Y)-H(Y|X)\]
还是上面的例子:
\(H(Y)=1\)
\(H(Y|X)=0.5\)
所以，\(IG(Y|X)=1-0.5=0.5\)
Relative Information Gain (相对信息增益)就是当需要传输\(Y\)的时候，通信两边都知道随机变量\(X\)的时候，平均每个字符可以节省的比特数占总的Entropy的比例。
\[RIG(Y|X)=(H(Y)-H(Y|X))/H(Y)\]

Information Gain具体有什么用？最直接的用处就是，当有一系列输入属性(features or attributes)\({x_{1}, x_{2}, ..., x_{n}}\)与你的目标属性\(Y\)相关，可以用Information Gain来发掘哪一个输入属性，包含了较多的目标属性的信息量，也意味着这个属性可以更好的来预测目标属性。
举个例子来说，为了预测是否一个人可以活到80岁,从以往的历史数据看
\(IG(LongLife|HairColor)=0.01\)
\(IG(LongLife|Smoker) = 0.2\)
\(IG(LongLife| Gender) = 0.25\)
\(IG(LongLife| LastDigitOfSSN) = 0.00001\)
从这四个属性{HairColor, Smoker, Gender, LastDigitOfSSN的信息增益可以看出，Gender(性别)与长寿更相关。

从以上可以看出，Information Gain是一个很好的工具用来预测特定的目标，由此延伸出一个机器学习方法－Decision Tree(决策树）。


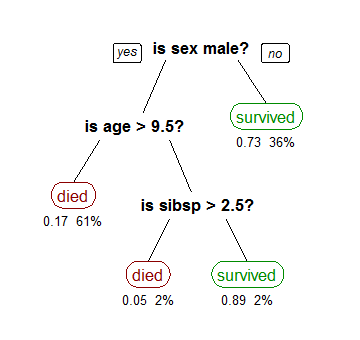
我们可以定义样本为:\((x,Y)=(x_{1},x_{2},x_{3},...,x_{k}, Y)\)，其中\(Y\) 是我们试图预测的目标属性，向量\(x\)是一系列不同的属性组合而成。而决策树的目标就是创造一个模型树根据输入属性预测目标属性的值。基本思想就是先计算所有不同属性的Information Gain，既\(IG(Y|x)\)。含有最大的Information Gain输入属性就可以作为Decision Tree的根，然后这样依此递归计算Information Gain,就可以得到一个Decision Tree，如上图所示，其中树的内部节点就是输入属性，树的边就是输入属性的可能值，数的叶子就是需要预测目标属性的值。

Regerence:
Entropy, wiki, 2011
Self-Informationlecture notes of R.Victor Jones, 2011
Decision Tree Learning, wiki, 2011
克劳德.香农， 百度百科，http://baike.baidu.com/view/63224.htm
Claude Elwood Shannon，wiki, 2011
Information Gain, Andrew's tutorials, 2011

MTX Operate System --- Introduction

本文的主要资料来自于Washington State University的操作系统课CS460和CS560.
参考资料：
《The Design of the UNIX Operating Systeem》 Maurice J. Bach, Prentice-Hall, Inc. 1986

这个笔记主要是为了自己复习和总结一下UNIX内核的知识，同时也想借此机会把国外优秀的课程介绍给国内的学生。

图1描述了UNIX系统的系统架构。

中间的硬件层(hardware)为操作系统提供了各种基本的服务。操作系统内核(kernel)把硬件层和应用层分离开来。这样做的好处使应用程序可以运行在不同的硬件上，所有与硬件有关的活动，都由操作系统来完成。各种应用程序如果需要硬件服务(读写文件 等)，则是通过系统调用(system call)告诉系统内核，然后系统内核操作硬件来完成服务。

图2 系统内核结构图

图2 主要展示了计算机系统的三层结构图: 用户层，内核层和 硬件层。用户层主要通过系统调用和库函数与内核交流。系统调用在内核里主要与文件子系统和进程控制子系统交互。

文件子系统主要负责管理文件，分配文件空间，控制文件访问权限，提取文件给用户。内核可以直接从硬盘读写数据，但是从硬盘读写数据要受到硬盘读写效率的限制。所以，系统内核需要对硬盘读写的频率进行优化，方法就是用一个缓冲区来存放经常被读写的数据。如果数据已经在缓冲区了，就不需要在到硬盘里去寻找了。

进程控制子系统主要负责进程同步，进程间互相通信，内存管理和进程调度。每一项都有很多细节要考虑和设计，以后的章节会详细介绍。

CASASviz: new version 1.0

The new version of our CASASviz has just been generated.

There are some major improvements:

1) Generate Main Visualizer by JavaScript Library Raphaël. We test our webpage on the PC and Iphone platform. There is no any delay. It works very well.

2) Use a web application model Comet to push the data from server to the browsers, without any request from the browsers.

3) Implement Pattern Visualization. Now we can show all kinds of the patterns based on different algorithms.

4) More Intelligent Functions:
1) Location Detection: show current room
2) Activity Level: use sliding time window to show the level of the activity
3) Enter or Leave Home Detection: use special rule
4) Activity Recognition: We are trying to use real-time activity recognition algorithm

Next Steps:
1) Polish our webpage for PC and Iphone platforms
2) Interview the caregivers to get some valuable suggestions

函数将字符串中的字符'*'移到串的前部分， 前面的非'*'字符后移，但不能改变非'*'字符的先后顺序，函数返回串中字符'*'的数量。

如原始串为：ab**cd**e*12，
处理后为*****abcde12，函数并返回值为5。（要求使用尽量少的时间和辅助空间）

这个题需要用到两个额外的下标而且要从后往前查找：第二个下标先找到第一个‘*’的位置，第一个下标，找到第一个'*'后面的字母，交换其中的字母；然后第二个下标指向下一个字符，第一个下标找到下一个字母，继续交换。
Time: O(n)

Common ancestor in a binary tree

From: http://zhedahht.blog.163.com/

第一变种是二叉树是一种特殊的二叉树：查找二叉树。也就是树是排序过的，位于左子树上的结点都比父结点小，而位于右子树的结点都比父结点大。我们只需要从根结点开始和两个结点进行比较。如果当前结点的值比两个结点都大，则最低的共同父结点一定在当前结点的左子树中。如果当前结点的值比两个结点都小，则最低的共同父结点一定在当前结点的右子树中。

第二个变种是树不一定是二叉树，每个结点都有一个指针指向它的父结点。于是我们可以从任何一个结点出发，得到一个到达树根结点的单向链表

现在我们回到这个问题本身。所谓共同的父结点，就是两个结点都出现在这个结点的子树中。因此我们可以定义一函数，来判断一个结点的子树中是不是包含了另外一个结点。这不是件很难的事，我们可以用递归的方法来实现：




我们可以从根结点开始，判断以当前结点为根的树中左右子树是不是包含我们要找的两个结点。如果两个结点都出现在它的左子树中，那最低的共同父结点也出现在它的左子树中。如果两个结点都出现在它的右子树中，那最低的共同父结点也出现在它的右子树中。如果两个结点一个出现在左子树中，一个出现在右子树中，那当前的结点就是最低的共同父结点。基于这个思路，我们可以写出如下代码：



接着我们来分析一下这个方法的效率。函数HasNode的本质就是遍历一棵树，其时间复杂度是O(n)（n是树中结点的数目）。由于我们根结点开始，要对每个结点调用函数HasNode。因此总的时间复杂度是O(n2)。

我们仔细分析上述代码，不难发现我们判断以一个结点为根的树是否含有某个结点时，需要遍历树的每个结点。接下来我们判断左子结点或者右结点为根的树中是否含有要找结点，仍然需要遍历。第二次遍历的操作其实在前面的第一次遍历都做过了。由于存在重复的遍历，本方法在时间效率上肯定不是最好的。



由于这个路径是从跟结点开始的。最低的共同父结点就是路径中的最后一个共同结点：



有了前面两个子函数之后，求两个结点的最低共同父结点就很容易了。我们先求出从根结点出发到两个结点的两条路径，再求出两条路径的最后一个共同结点。代码如下：



这种思路的时间复杂度是O(n)，时间效率要比第一种方法好很多。但同时我们也要注意到，这种思路需要两个链表来保存路径，空间效率比不上第一个方法。

Convert Sorted List to Balanced Binary Search Tree (BST)

Things get a little more complicated when you have a singly linked list instead of an array. Please note that in linked list, you no longer have random access to an element in O(1) time.


Singly-linked lists contain nodes which have a data field as well as a next field, which points to the next node in the linked list.
Naive Solution:
A naive way is to apply the previous solution directly. In each recursive call, you would have to traverse half of the list’s length to find the middle element. The run time complexity is clearly O(N lg N), where N is the total number of elements in the list. This is because each level of recursive call requires a total of N/2 traversal steps in the list, and there are a total of lg N number of levels (ie, the height of the balanced tree).

Hint:
How about inserting nodes following the list’s order? If we can achieve this, we no longer need to find the middle element, as we are able to traverse the list while inserting nodes to the tree.

Best Solution:
As usual, the best solution requires you to think from another perspective. In other words, we no longer create nodes in the tree using the top-down approach. We create nodes bottom-up, and assign them to its parents. The bottom-up approach enables us to access the list in its order while creating nodes.

Isn’t the bottom-up approach neat? Each time you are stucked with the top-down approach, give bottom-up a try. Although bottom-up approach is not the most natural way we think, it is extremely helpful in some cases. However, you should prefer top-down instead of bottom-up in general, since the latter is more difficult to verify in correctness.

Below is the code for converting a singly linked list to a balanced BST. Please note that the algorithm requires the list’s length to be passed in as the function’s parameters. The list’s length could be found in O(N) time by traversing the entire list’s once. The recursive calls traverse the list and create tree’s nodes by the list’s order, which also takes O(N) time. Therefore, the overall run time complexity is still O(N).

Convert Sorted Array to Balanced Binary Search Tree (BST) 把已排序的数组转换成平衡二叉搜索树

A height-balanced tree is a tree whose subtrees differ in height by no more than one and the subtrees are height-balanced, too.

Solution:
If you would have to choose an array element to be the root of a balanced BST, which element would you pick? The root of a balanced BST should be the middle element from the sorted array.

You would pick the middle element from the sorted array in each iteration. You then create a node in the tree initialized with this element. After the element is chosen, what is left? Could you identify the sub-problems within the problem?

There are two arrays left — The one on its left and the one on its right. These two arrays are the sub-problems of the original problem, since both of them are sorted. Furthermore, they are subtrees of the current node’s left and right child.

The code below creates a balanced BST from the sorted array in O(N) time (N is the number of elements in the array). Compare how similar the code is to a binary search algorithm. Both are using the divide and conquer methodology.

Find paths in a binary tree summing to a target value

Given a binary tree, write a function to find the length of the longest path in the tree.

Input: Binary Tree
10
/ \
6 14
/ / \
4 12 16
The depth of the tree is 3.





Recursive Solution:

Mirror image of binary search tree?

题目：输入一颗二元查找树，将该树转换为它的镜像，即在转换后的二元查找树中，左子树的结点都大于右子树的结点。用递归和循环两种方法完成树的镜像转换。 例如输入：
8
/ \
6 10
/\ /\
5 7 9 11
输出：
8
/ \
10 6
/\ /\
11 9 7 5
定义二元查找树的结点为：


Recursive solution:
We can use in-order traversal to implement recursive function.


Non-recursive solution: use stack to simulate the recursive

Check if a binary tree is BST or not 检查一个二叉树是不是二叉搜索书

Best Solution:
1) Do In-Order Traversal of the given tree and store the result in a temp array.
3) Check if the temp array is sorted in ascending order, if it is, then the tree is BST.

Time Complexity: O(n)
Auxiliary Space: O(n)

Verify whether a squence of integers are the post order traversal of a binary search tree (BST)

A binary search tree (BST) is a node based binary tree data structure which has the following properties.
• The left subtree of a node contains only nodes with keys less than the node’s key.
• The right subtree of a node contains only nodes with keys greater than the node’s key.
• Both the left and right subtrees must also be binary search trees.

From the above properties it naturally follows that:
• Each node (item in the tree) has a distinct key.

Printing BFS (Binary Tree) in Level Order

Solution 1: iterative


First of all, we implement this function PrintNodeAtLevel




Then, we can travel all the level of the tree




The problem of the first solution is that it repeat traveling the tree from the root every time. To avoid the repeat computation, we can use an queue to put the nodes into the queue one by one.

How to Rebuild a binary tree from Inorder and Preorder traversals ?

This link is a tutorial.

Recursive Solution:

Find nodes with longest distance in Binary Tree

Recursive Solution:

Convert a string to integer？ 把一个字符串转换成整数？

Input a string, output the maximum length of symmetrical substring 输入一个字符串，输出该字符串中对称的子字符串的 最大长度

From: http://zhedahht.blog.163.com/。整理出版物请和作者联系。


比如输入字符串“google”，由于该字符串里最长的对称子字符串是“goog”，因此输出4.
For example, input the string "google", the maximum length of symmetrical substring is "goog", then output 4.

要判断一个字符串是不是对称的，不是一件很难的事情。我们可以先得到字符串首尾两个字符，判断是不是相等。如果不相等，那该字符串肯定不是对称的。否则我们接着判断里面的两个字符是不是相等，以此类推。基于这个思路，我们不难写出如下代码：
It is not very difficult to determine whether or not a string is symmetrical. We can compare the symbols from the begin and end of the string, to see whether they are equal. If they are not equal, this string is not symmetrical. If they are equal, we can continue to compare the inner symbols. Based upon this idea, the code can be described as follows:


要判断一个字符串pString是不是对称的，我们只需要调用IsSymmetrical(pString, &pString[strlen(pString) – 1])就可以了。
To determine whether a string pString is symmetrical, we

现在我们试着来得到对称子字符串的最大长度。最直观的做法就是得到输入字符串的所有子字符串，并逐个判断是不是对称的。如果一个子字符串是对称的，我们就得到它的长度。这样经过比较，就能得到最长的对称子字符串的长度了。于是，我们可以写出如下代码：


我们来分析一下上述方法的时间效率。由于我们需要两重while循环，每重循环需要O（n）的时间。另外，我们在循环中调用了IsSymmetrical，每次调用也需要O（n）的时间。因此整个函数的时间效率是O（n3）。
There are two "while' loop in the code. In every loop, we should use IsSymetrical funtion, which also needs O(n) time. The total time performance is O(n^3).

通常O（n3）不会是一个高效的算法。如果我们仔细分析上述方法的比较过程，我们就能发现其中有很多重复的比较。假设我们需要判断一个子字符串具有aAa的形式（A是aAa的子字符串，可能含有多个字符）。我们先把pFirst指向最前面的字符a，把pLast指向最后面的字符a，由于两个字符相同，我们在IsSymtical函数内部向后移动pFirst，向前移动pLast，以判断A是不是对称的。接下来若干步骤之后，由于A也是输入字符串的一个子字符串，我们需要再一次
判断它是不是对称的。也就是说，我们重复多次地在判断A是不是对称的。
Usually, O(n^3) is not an effective algorithm. If we carefully analyze the process of the comparison, many repeated comparison can be found. For example, if we determine the symmetry of the substring aAa, we should compare aA firstly, and then compare aAa. However, after that, we will continue to compare Aa and a, which is not necessary to compare them again.

造成上述重复比较的根源在于IsSymmetrical的比较是从外向里进行的。在判断aAa是不是对称的时候，我们不知道A是不是对称的，因此需要花费O（n）的时间来判断。下次我们判断A是不是对称的时候，我们仍然需要O（n）的时间。
The main reason leading to the repeated comparison is that we compare the string from the outer to the inner. When checking the symmetry of aAa, we don't know whether A is symmetrical. It still costs O(n) to determine it.

如果我们换一种思路，我们从里向外来判断。也就是我们先判断子字符串A是不是对称的。如果A不是对称的，那么向该子字符串两端各延长一个字符得到的字符串肯定不是对称的。如果A对称，那么我们只需要判断A两端延长的一个字符是不是相等的，如果相等，则延长后的字符串是对称的。因此在知道A是否对称之后，只需要O（1）的时间就能知道aAa是不是对称的。
we can change our mine to determine the symmetry from the inner to the outer. We can check whether the substring A is symmetrical. If not, the extension of this substring is definitively not symmetrical. If A is symmetrical, the only thing we can do is to check the extension of A is symmetrical. Thus, the time performance of o(1) is needed to check wheterh aAa is symmetrical. The code is as follows:

我们可以根据从里向外比较的思路写出如下代码：

由于子字符串的长度可能是奇数也可能是偶数。长度是奇数的字符串是从只有一个字符的中心向两端延长出来，而长度为偶数的字符串是从一个有两个字符的中心向两端延长出来。因此我们的代码要把这种情况都考虑进去。

在上述代码中，我们从字符串的每个字符串两端开始延长，如果当前的子字符串是对称的，再判断延长之后的字符串是不是对称的。由于总共有O（n）个字符，每个字符可能延长O（n）次，每次延长时只需要O（1）就能判断出是不是对称的，因此整个函数的时间效率是O（n2）。

Write a strcpy function 如何写strcpy函数

char *strcpy(char *strDest, const char *strSrc);
其中strDest 是目的字符串，strSrc 是源字符串。



strcpy能把strSrc的内容复制到strDest，为什么还要char * 类型的返回值？

答：为了实现链式表达式。 // 2分

例如 int length = strlen( strcpy( strDest, “hello world”) );

Write a function to determine is a string is an anagram of a palindrome 写一个函数判断一个字符串是不是回文结构

c++ version


c version

Reverse a String 如何反转一个字符串

x[i]= a;
x[j] = b;
x[j]=a xor b;
x[i]= x[i] xor x[j] = a xor ( a xor b) = b;
x[j]= x[j] xor x[i] = a xor b xor b = a;

==> xor b; x[i]=axorb ==> xor b

no need extra space

Input two strings, delete all the symbols of the first strings, which appear in the second string输入两个字符串，从第一字符串中删除第二个字符串中所有的字符。

For example, the first string "They are students" and the second string "aeiou";

after deleting, the first string is "Thy r stdents."

例如，输入”They are students.”和”aeiou”，

则删除之后的第一个字符串变成”Thy r stdnts.”

首先我们考虑如何在字符串中删除一个字符。由于字符串的内存分配方式是连续分配的。我们从字符串当中删除一个字符，需要把后面所有的字符往前移动一个字节 的位置。但如果每次删除都需要移动字符串后面的字符的话，对于一个长度为 n 的字符串而言，删除一个字符的时间复杂度为 O(n) 。而对于本题而言，有可能要 删除的字符的个数是 n ，因此该方法就删除而言的时间复杂度为 O(n2) 。

事实上，我们并不需要在每次删除一个字符的时候都去移动后面所有的字符。我们可以设想，当一个字符需要被删除的时候，我们把它所占的位置让它后面的字符来 填补，也就相当于这个字符被删除了。在具体实现中，我们可以定义两个指针 (pFast 和 pSlow) ，初始的时候都指向第一字符的起始位置。当 pFast 指向的字符是需要删除的字符，则 pFast 直接跳过，指向下一个字符。如果 pFast 指向的字符是不需要删除的字符，那么把 pFast 指向的字符赋值给 pSlow 指向的字符，并且 pFast 和 pStart 同时向后移动指向下一个字符。这样，前面被 pFast 跳过的字符相当于被删除了。用这种方法，整个删 除在 O(n) 时间内就可以完成。

接下来我们考虑如何在一个字符串中查找一个字符。当然，最简单的办法就是从头到尾扫描整个字符串。显然，这种方法需要一个循环，对于一个长度为 n 的字符串，时间复杂度是 O(n) 。

由于字符的总数是有限的。对于八位的 char 型字符而言，总共只有 28=256 个字符。我们可以新建一个大小为 256 的数组，把所有元素都初始化为 0 。然 后对于字符串中每一个字符，把它的 ASCII 码映射成索引，把数组中该索引对应的元素设为１。这个时候，要查找一个字符就变得很快了：根据这个字符的 ASCII 码，在数组中对应的下标找到该元素，如果为 0 ，表示字符串中没有该字符，否则字符串中包含该字符。此时，查找一个字符的时间复杂度是 O(1) 。 其实，这个数组就是一个 hash 表。

Write C code to implement the strstr() (search for a substring) function. 用c语言实现strstr()函数

Method1

The first method is the classic Brute force method. The Brute Force algorithm checks, at all positions in the text between 0 and (n-m), if an occurrence of the pattern starts at that position or not. Then, after each successfull or unsuccessful attempt, it shifts the pattern exactly one position to the right. The time complexity of this searching phase is O(mn). The expected number of text character comparisons is 2n.

Here 'n' is the size of the string in which the substring of size 'm' is being searched for.



Method2

The second method is called the Rabin-Karp method.

Instead of checking at each position of the text if the pattern occurs or not, it is better to check first if the contents of the current string "window" looks like the pattern or not. In order to check the resemblance between these two patterns, a hashing function is used. Hashing a string involves computing a numerical value from the value of its characters using a hash function.

The Rabin-Karp method uses the rule that if two strings are equal, their hash values must also be equal. Note that the converse of this statement is not always true, but a good hash function tries to reduce the number of such hash collisions. Rabin-Karp computes hash value of the pattern, and then goes through the string computing hash values of all of its substrings and checking if the pattern's hash value is equal to the substring hash value, and advancing by 1 character every time. If the two hash values are the same, then the algorithm verifies if the two string really are equal, rather than this being a fluke of the hashing scheme. It uses regular string comparison for this final check. Rabin-Karp is an algorithm of choice for multiple pattern search. If we want to find any of a large number, say k, fixed length patterns in a text, a variant Rabin-Karp that uses a hash table to check whether the hash of a given string belongs to a set of hash values of patterns we are looking for. Other algorithms can search for a single pattern in time order O(n), hence they will search for k patterns in time order O(n*k). The variant Rabin-Karp will still work in time order O(n) in the best and average case because a hash table allows to check whether or not substring hash equals any of the pattern hashes in time order of O(1).



Method3

The Knuth-Morris-Pratt or the Morris-Pratt algorithms are extensions of the basic Brute Force algorithm. They use precomputed data to skip forward not by 1 character, but by as many as possible for the search to succeed.

Counting frequency of a substring in a string 计算字符串中子字符串出现的频率在

A suffix tree can take slightly more memory (still linear, though) than a suffix array, but is easier to implement to build quickly since you can use something like a radix sort idea as you add things to the tree (see the wikipedia link from the name for details).
The KMP algorithm is also good to be aware of, which is specialized for searching for a particular substring within a longer string very quickly. If you only need this special case, just use KMP and no need to bother building an index of suffices first.

String Concatenation with Overlap 两个字符串首尾相连的有多少字符重合

Consider Knuth Morris Pratt. It keeps track of the maximum amount of substring we have matched so far throughout. That means it knows how much of S1 has been matched at the end of S2, and that's the value we're looking for! Just modify the algorithm to continue instead of returning when it matches the substring early on, and have it return the amount matched instead of 0 at the end.

That gives you an O(n) algorithm. Nice!

Concatenation of two linked lists

Find Longest Common Substring 查找字符串中最长公共字串

Basically two ways:
1.dynamic programming, which cost O(mn) time and O(mn) space.

2. suffix tree, by this you need to build it first, the building process with suffix link is O(m+n) (time and space), if without suffix link is O((m+n)^2) (time). Though building the suffix tree process is of same efficiency with dynamic programming in best case, however, after you have built it, you could get the longest common substring in O(k) time (k is the length of the LCS).

Print out all the permutations of a string

我们以三个字符abc为例来分析一下求字符串排列的过程。首先我们固定第一个字符a，求后面两个字符bc的排列。当两个字符bc的排列求好之后，我们把第一个字符a和后面的b交换，得到bac，接着我们固定第一个字符b，求后面两个字符ac的排列。现在是把c放到第一位置的时候了。记住前面我们已经把原先的第一个字符a和后面的b做了交换，为了保证这次c仍然是和原先处在第一位置的a交换，我们在拿c和第一个字符交换之前，先要把b和a交换回来。在交换b和a之后，再拿c和处在第一位置的a进行交换，得到cba。我们再次固定第一个字符c，求后面两个字符b、a的排列。

Find the longest numeric string in a string, return the length of this string

Input: "abcd12345ed125ss123456789"
Return: the length of "123456789"

Given two string s1 and s2 how will you check if s1 is a rotated version of s2 ?

我们还是把字符串看成有两段组成的，记位XY。左旋转相当于要把字符串XY变成YX。我们先在字符串上定义一种翻转的操作，就是翻转字符串中字符的先后顺序。把X翻转后记为XT。显然有(XT)T=X。

我们首先对X和Y两段分别进行翻转操作，这样就能得到XTYT。接着再对XTYT进行翻转操作，得到(XTYT)T=(YT)T(XT)T=YX。正好是我们期待的结果。

分析到这里我们再回到原来的题目。我们要做的仅仅是把字符串分成两段，第一段为前面m个字符，其余的字符分到第二段。再定义一个翻转字符串的函数，按照前面的步骤翻转三次就行了。时间复杂度和空间复杂度都合乎要求。

Convert string to numeric value

Chinese version: http://hi.baidu.com/mycollection/blog/item/9b37aa5167bdb213367abeb8.html

分析：这道题尽管不是很难，学过C/C++语言一般都能实现基本功能，但不同程序员就这道题写出的代码有很大区别，可以说这道题能够很好地反应出程序员的思维和编程习惯，因此已经被包括微软在内的多家公司用作面试题。建议读者在往下看之前自己先编写代码，再比较自己写的代码和下面的参考代码有哪些不同。

首先我们分析如何完成基本功能，即如何把表示整数的字符串正确地转换成整数。还是以"345"作为例子。当我们扫描到字符串的第一个字符'3'时，我们不知道后面还有多少位，仅仅知道这是第一位，因此此时得到的数字是3。当扫描到第二个数字'4'时，此时我们已经知道前面已经一个3了，再在后面加上一个数字4，那前面的3相当于30，因此得到的数字是3*10+4=34。接着我们又扫描到字符'5'，我们已经知道了'5'的前面已经有了34，由于后面要加上一个5，前面的34就相当于340了，因此得到的数字就是34*10+5=345。

分析到这里，我们不能得出一个转换的思路：每扫描到一个字符，我们把在之前得到的数字乘以10再加上当前字符表示的数字。这个思路用循环不难实现。

由于整数可能不仅仅之含有数字，还有可能以'+'或者'-'开头，表示整数的正负。因此我们需要把这个字符串的第一个字符做特殊处理。如果第一个字符是'+'号，则不需要做任何操作；如果第一个字符是'-'号，则表明这个整数是个负数，在最后的时候我们要把得到的数值变成负数。

接着我们试着处理非法输入。由于输入的是指针，在使用指针之前，我们要做的第一件是判断这个指针是不是为空。如果试着去访问空指针，将不可避免地导致程序崩溃。另外，输入的字符串中可能含有不是数字的字符。每当碰到这些非法的字符，我们就没有必要再继续转换。最后一个需要考虑的问题是溢出问题。由于输入的数字是以字符串的形式输入，因此有可能输入一个很大的数字转换之后会超过能够表示的最大的整数而溢出。

现在已经分析的差不多了，开始考虑编写代码。首先我们考虑如何声明这个函数。由于是把字符串转换成整数，很自然我们想到：

int StrToInt(const char* str);

这样声明看起来没有问题。但当输入的字符串是一个空指针或者含有非法的字符时，应该返回什么值呢？0怎么样？那怎么区分非法输入和字符串本身就是”0”这两种情况呢？

接下来我们考虑另外一种思路。我们可以返回一个布尔值来指示输入是否有效，而把转换后的整数放到参数列表中以引用或者指针的形式传入。于是我们就可以声明如下：

bool StrToInt(const char *str, int& num);

这种思路解决了前面的问题。但是这个函数的用户使用这个函数的时候会觉得不是很方便，因为他不能直接把得到的整数赋值给其他整形变脸，显得不够直观。

前面的第一种声明就很直观。如何在保证直观的前提下当碰到非法输入的时候通知用户呢？一种解决方案就是定义一个全局变量，每当碰到非法输入的时候，就标记该全局变量。用户在调用这个函数之后，就可以检验该全局变量来判断转换是不是成功。

Find the first un-repeated character in a string

Chinese version： http://hi.baidu.com/mycollection/blog/item/962571630f017d6b0c33fa39.html
看到这道题时，最直观的想法是从头开始扫描这个字符串中的每个字符。当访问到某字符时拿这个字符和后面的每个字符相比较，如果在后面没有发现重复的字符，则该字符就是只出现一次的字符。如果字符串有n个字符，每个字符可能与后面的O(n)个字符相比较，因此这种思路时间复杂度是O(n2)。我们试着去找一个更快的方法。

由于题目与字符出现的次数相关，我们是不是可以统计每个字符在该字符串中出现的次数？要达到这个目的，我们需要一个数据容器来存放每个字符的出现次数。在这个数据容器中可以根据字符来查找它出现的次数，也就是说这个容器的作用是把一个字符映射成一个数字。在常用的数据容器中，哈希表正是这个用途。

哈希表是一种比较复杂的数据结构。由于比较复杂，STL中没有实现哈希表，因此需要我们自己实现一个。但由于本题的特殊性，我们只需要一个非常简单的哈希表就能满足要求。由于字符（char）是一个长度为8的数据类型，因此总共有可能256 种可能。于是我们创建一个长度为256的数组，每个字母根据其ASCII码值作为数组的下标对应数组的对应项，而数组中存储的是每个字符对应的次数。这样我们就创建了一个大小为256，以字符ASCII码为键值的哈希表。

我们第一遍扫描这个数组时，每碰到一个字符，在哈希表中找到对应的项并把出现的次数增加一次。这样在进行第二次扫描时，就能直接从哈希表中得到每个字符出现的次数了。

Reverse words in sentence while keeping position of white space

Input: “I am a student."
Output: “student. a am I"
Time: O(n).

Solution: At the first step, reverse the whole sentence, then reverse the word one by one.

Fibonacci Number

/ 0, n = 0
f(n)- 1, n = 1
\ f(n-1)+f(n-2), n = 2

Given an array of numbers, return maximum products of all possible n-1 numbers

Solution 1:

set array[] as initial array;
s[i] represents the product of the first i numbers

s[0] = 1 is the boundary, Thus s[i]=s[i-1]*array[i-1], 1 <= i <= N; t[i] represents the product of the last (N-i) numbers
t[N+1] = 1 is also the boundary;
Thus, t[i]=t[i+1]*array[i],1 <= i <= N;

set p[i] is the product of N-1 numbers except the number i.
p[i]=s[i-1]*t[i+1]

Searching from the begin to the end, we can get the array s[]; Searching from the end to the begin, we can get the array t[]. In the linear time, we can get p[]. The maximum value of p[] is what we need.

Solution2: Support P is the product of total N numbers;
There are three cases:
1) P is 0: That means there is at least one 0 in the array. If we remove one 0, the product of other N-1 numbers is Q.
1.1 Q is 0. That means the array has at least two 0. The product of N-1 numbers is just 0.
1.2 Q > 0. Return Q.
1.3 Q < 0. Return 0.

2) P < 0. We will remove a negative number from the array. To get the biggest product of N-1 number, we had to remove the minimum absolute value during all the negative numbers.

3) P > 0. We will remove the minimum absolute value during all the positive numbers.

Return top k values from an array of length N

Best solution: We can use the heap of length k to store the top k values. The smallest value Y is on the top of the heap. When considering a new value X, if X <= Y, we don't need to change the original heap. If X > Y, X should replace Y on the heap and then we need to update the heap again. The update algorithm is O(logK).

The time of this algorithm is O(n*logK).

The definition of the heap: http://en.wikipedia.org/wiki/Heap_(data_structure)

How to update the min-heap:


If N is positive integer, the range is not very big. We can consider use extra space counte[MAXN] to record the frequency of the integer, then pick up the top k frequency numbers.

Finding Maximum/Minimum Value in an Array

Solution 1: If we just travel the whole array, find out the maximum and minimum number.
We need to compare 2*N times to find out the maximum and minimum number.

Solution 2: We put two neighbors in the array into one group, then use Max and Min variable to store the current max and min value. Then, we travel to the next group. If the min value in the next group is smaller than the Min variable and update Min variable. We update Max variable using the same way. We repeat the same process in the whole array.

We need to compare 1.5*N times.

Given a sorted array of integers, how can you find the location of a particular integer x?

Best Solution: Binary Search O(Logn)

Check whether there is a cycle in the linked list(检查链表里是否有环).

Set two pointers(fast, slow) both points the head of the linked list. The slow pointer moves one step, and the fast pointer moves two steps. If there is a cycle, the fast pointer will meet the slow pointer. The program is as follows:



How to find out the entrance of the cycle?

If we found the cycle in the linked list, we let p2 come back to the head of the linked list and go ahead, however, the length of the step should be one. When the meet with P1 and P2, that is the entrance of the cycle.

Chinese Prove:
在p2和p1第一次相遇的时候，假定p1走了n步骤，环路的入口是在p步的时候经过的，那么有

p1走的路径： p+c ＝ n； c为p1和p2相交点，距离环路入口的距离

p2走的路径： p+c+k*L = 2*n； L为环路的周长，k是整数

显然，如果从p+c点开始，p1再走n步骤（即k*L步，p1又循环了k圈）的话，还可以回到p+c这个点

同时p2从头开始走的话，经过n步，也会达到p+c这点

显然在这个步骤当中p1和p2只有前p步骤走的路径不同，所以当p1和p2再次重合的时候，必然是在链表的环路入口点上。

From Chinese version: http://blog.csdn.net/sayigood/archive/2009/02/15/3891735.aspx

Copy Complex Node

Given a complex node, one pointer m_pNext points to the next node, and the other pointer m_pSibling points to the random node or NULL in the linked list. How to copy this complex linked list? Function: ComplexNode* Clone(ComplexNode* pHead).




The the first solution: use O(n) space to implement O(n) time performance.
The first step copys every node N of the linked list to a new node N', then connect all of these new nodes together. The trick is to build a haspmap stored into a pair . The second step is to find the corresponding node to copy the m_pSibling node of original linked list. Due to the hashmap, we can use O(1) to find S' from S.

The second solution is to implement O(n) performance without using additional space O(n).

In first step, we still copy a new node N' corresponding to the node N of original linked list. However, we put the N' back to the N as the following graph:





The second step is to copy the m_pSibling node of the original linked list. If the m_pSibling pointer of the node N of the original linked list points to S, then the m_pSibling pointer of the correspoinding node N' points to S' like the following graph.





The last step is to divide this linked list into two separate parts: the odd nodes belong to the original linked list; the even nodes belong to the new linked list.





The whole process is:


From Chinese version: http://zhedahht.blog.163.com/

Given a sorted array A[1..n] with n integers, and an integer t, find all pairs (x,y) of elements in A such that x+y is smaller than t. 2. Can we do

Array A[i...n]. t is the given value.
Create a hash of size t assuming t <= n and 1 < t.
Iterate the array to create a hash O(t) (t < n).
The key of the hash should be the value A[i] and value of the hash should be (t - A[i]).

Iterate again over the array again (which is O(t)).
Look up every key in hash matching the value of A[i]. Check if there is an existing key in the hash table which matches value of the A[i].

The hash lookups are constant time. The overall complexity is 2n.

Given a pointer to a node (not the tail node) in a singly linked list. Delete that node from the linked list.

Solution: move the data from the next node into the current node and then deleting the next node. This solution has O(1) runtime.



只给定单链表中某个结点p(非空结点)，在p前面插入一个结点。

办法与前者类似，首先分配一个结点q，将q插入在p后，接下来将p中的数据copy入q中，然后再将要插入的数据记录在p中。

Merging two sorted linked lists

Solution: First of all, compare with each node of two linked list, then insert one by one into a new linked list.

Reverse a Linked-List

Solution: The easiest way is to delete the node one by one, and then create a new linked list to connect the nodes in another direction.

Find kth node of a linked list from end

Solution:
When we travel the linked list, we can keep two pointers. The first pointer moves k steps and the second pointer begins to move. The distance of two pointers are always k-1 steps. When the first pointer arrives at the end of the linked list, the second pointer is pointing the kth node from end.

Time: O(n)



The other similar question:

输入一个单向链表。如果该链表的结点数为奇数，输出中间的结点；如果链表结点数为偶数，输出中间两个结点前面的一个。

Check whether there is the intersection of two linked lists

Given the heads of two linked lists, judge whether there is the intersection of two linked list.

Extend Question:
1. If there is a ring in the linked list, how do you change?
2. Can you find the first intersection node?

Two solutions:
1. We can connect the head of the second linked list to the tail of the first linked list. If there is a ring existing into the new linked list, two linked lists intersects.
Thus, we translated the problem into another problem that checks there is the ring of two linked lists.

2. Firstly, we can travel the first linked list and remember the last node, then travel the next linked list to get the last node. We compare the two last nodes. If they are the same, two linked list intersects.
Time: O(Length(h1)+Length(h2))

After we travels two linked lists, we attain their lengths of two linked lists. The longer one moves (LengthMax - LengthMin), then two linked list move together. If they can find the first same node, it should be the first node they intersects.

Convert a binary search tree into sorted double link list

For example, binary search tree
10
/ \
6 14
/\ /\
4 8 12 16
into double link list:
4=6=8=10=12=14=16

Idea:
The basic idea is that we can get the sorted the elements in the tree by in-order traveling. When we visit one node, we can put this node into the double link list. After traveling the whole tree, we can get a sorted double link list.

The code is as follows:

CASASviz: New Requirements from the Caregivers

At Feb 9th, Heidi, Prafulla and I went to Aging Heath Center at Moscow for inquiring their real needs for our project. These caregivers are very friendly and excited about our project.

The following list is their requirement in need:
1) Anomaly detection: The most worry thing for the caregivers is the safety of the patient in the house. Thus, the safety is the top need for them.
* Leaving home, someone unfamiliar coming home
* Stove and faucet are left open
* Metal in the microwave
* Moving into some dangerous place
* Taking medicine in time

Solution: Based-Rule(Final State Machine) to detect these anomalies. However, we had to make the corresponding rules for them.

2) Monitoring the mobility and Recognizing Activities
* Monitoring the mobility in real time and reviewing history
* Recognize Activities and the Caregivers want to know whether some activities have been finished in right time.

3) Interface
They are very interested into our tool can be implemented on the platform of the smart phones.

CASASviz: Improvement (1)

Here is some improvement to be implemented into our CASASviz 2.0

1)To solve the visualize the data in real time, we will use Raphel SVG library to draw the main graph dynamically. (I already tested the graph. It works very well)

2)Prafulla is working on the client cache part, which will solve us the out-of-memory problem in server.

3)We are planning to apply real-time activity recognition algorithm into our webpage system.javascript:void(0)